打てる箇所の価値

このサイトを立ち上げて最初に書いたのは手番の価値という記事でした。中盤くらいまでの多くのケースで手番は相手に渡した方が得ということでしたが、手番が回ってこない方が打てる箇所を浪費しないで済む、というのが理由だと考えられます。今回は、もっと素朴に「打てる箇所の数」にはどれくらいの価値があるのかを考えてみたいと思います。

打てる場所が減ってくると当然取り得る選択肢も減り、嫌々な手を打たざるを得なくなる可能性も高まります。したがって自分と相手の打てる箇所がそれぞれいくつあるかがある程度試合の形勢を表しているのではないかと考えられます。では打てる箇所にどの程度の差がつくと、どの程度の形勢になるのでしょうか？もし仮に、打てる箇所1ヶ所は大体2石の価値があるということになれば、例えば自分の打てる箇所が10ヶ所、相手の打てる箇所が8箇所なら、自分が4石くらいリードしていると考えることができます。もちろん打てる箇所以外の要因もあるのでこんな単純な話ではないというのは重々承知はしていますが、「平均的にはこれくらい」という目安があるだけでも役に立つのではないかと考えました。

ネット上で探してみても、打てる箇所が1ヶ所あたり何石くらいに相当するというような情報は見当たりませんでした。実は「余裕手は百万ドルの価値」と言っているサイトは見つけたのですが、お金ではなく石数に換算したいのです(まぁ、全てお金に換算できるならそれでも良いのですけど(笑))。

ということで、今回の目標は「打てる箇所1ヶ所は何石の価値があるか」を求めることです。

例によってWTHORの棋譜がありますので、これを使って打てる箇所1ヶ所あたりの価値を求めたいと思います。打てる箇所の数と言っても、自分が打てる箇所と相手の打てる箇所があります。先ほど何となく例として書いたように、自分の打てる箇所数と相手の打てる箇所数の差が優劣に関係がありそうです。ただし、例えば打てる箇所数の差が2だとしても、「自分=14、相手=12」の時と「自分=4、相手=2」の時で優劣は大分違うようにも思われます。なので、自分と相手の打てる箇所数の差だけを見るのでなく、両方の値をきちんと見る必要がありそうです。

また、手番の価値の時もそうでしたが、序盤・中盤・終盤で価値が変わってくる可能性もあります。これも考慮することにすると、

• 自分の打てる箇所の数
• 相手の打てる箇所の数
• 何手目の局面か

のそれぞれの組み合わせについて評価値を調べることで、打てる箇所1ヶ所あたりの価値を求めてみたいと思います。

まずは、打てる箇所の数の分布がどうなっているかを見てから、何手目の局面かに対する依存性を見た上で、自分と相手の打てる箇所数が変わると評価値がどう変わるかを見るという流れで調査を進めていきたいと思います。

まずは、打てる箇所の数が手が進むにつれてどう推移するのかをWTHORに入っていた全日本選手権の1035試合の棋譜を使って調べてみました。 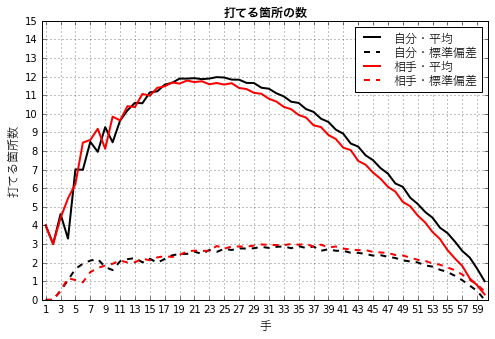このグラフは1手目〜60手目までで、自分(その局面の手番の人)の打てる箇所の数と、相手(手番でない人)の打てる箇所の数の、平均と標準偏差をプロットしたものです¹⁾。自分が黒いグラフ、相手が赤いグラフで、実線が平均、点線が標準偏差です。初手は両者とも4ヶ所ずつ打てる箇所があります。そして中盤にかけて平均12ヶ所くらいまで増えて、そこから終盤にかけて減っていくという形になっています。中盤以降は手番側の人の方が平均的に1ヶ所くらいずつ打てる箇所が多い状況で推移していくようです。そして標準偏差は最初のあたりと最後のあたりを除くと2〜3程度のようです。

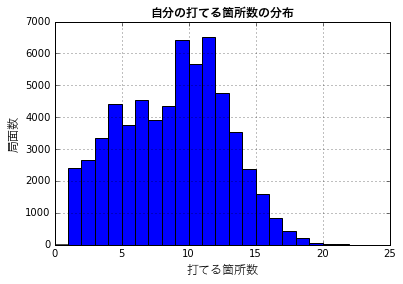
それぞれの分布についても見てみました。 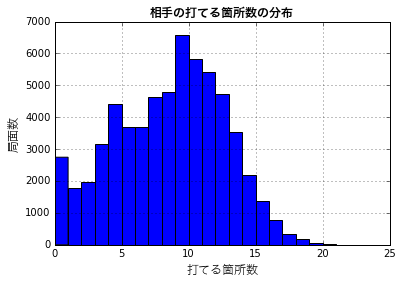15ヶ所を超えたあたりから出現回数が大分減ってくるようです。自分と相手の打てる箇所数の組み合わせごとの分布も見てみます。 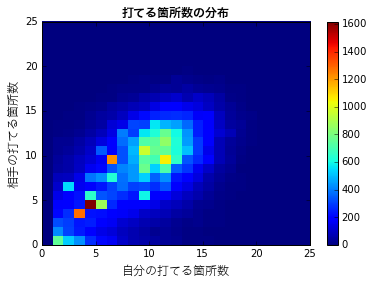赤や黄色が出現頻度の高いエリア、青に近づくほど出現頻度が低いエリアとなります。当然と言えば当然ですが、自分と相手の打てる箇所の数が同じくらいの局面は出現頻度が高く、差が開いていくにつれて出現頻度が減っています。自分と相手がともに4という組の出現頻度が高いのは、初期局面がこれに該当するからだと考えられます。両者とも10ヶ所前後のエリアもかなり多いようです。また、両者とも0〜2か所くらいのエリアも多いですが、これは最終盤はだいたいそうなるからだと思われます。色がうっすらとでも見える範囲は打てる箇所=19あたりまでのようなので、このあたりまでを調査対象としたいと思います。

打てる箇所数の分布がわかったので、手が進むにつれて打てる箇所数の価値がどう変わっていくかを見てみたいと思います。例えば、打てる箇所数が「自分=10、相手=10」の時の評価値と「自分=11、相手=10」の時の評価値を比べると、1箇所あたりの価値になるはずです。ただ、これを1手目から60手目までの1手ごとにやっていくと、1つ1つの組み合わせに該当する件数が少なくなりすぎて統計上の誤差が大きくなりそうですし、組み合わせがある程度得られたとしてもパラメータが多すぎて表なりグラフなりに表現するのが難しそうです。そこで、箇所数についてはまずは自分と相手の打てる箇所数の差だけを見ることにします。今は1手目から60手目までそれぞれで見ているので、先ほど見たように打てる箇所数の推移は概ね山なりで標準偏差も2〜3程度であり、打てる箇所数の絶対数はあまり大きくバラつきません。したがって差だけを見てもある程度意味のある結果が得られるのではないかと思ったからです。差が-2〜+2の範囲の局面の評価値についてそれぞれ平均と標準偏差を出し、グラフにプロットしてみました。本当はもう少し差を見る範囲を広げたかったのですが、グラフがごちゃごちゃしてしまうので-2〜+2の範囲にとどめました。 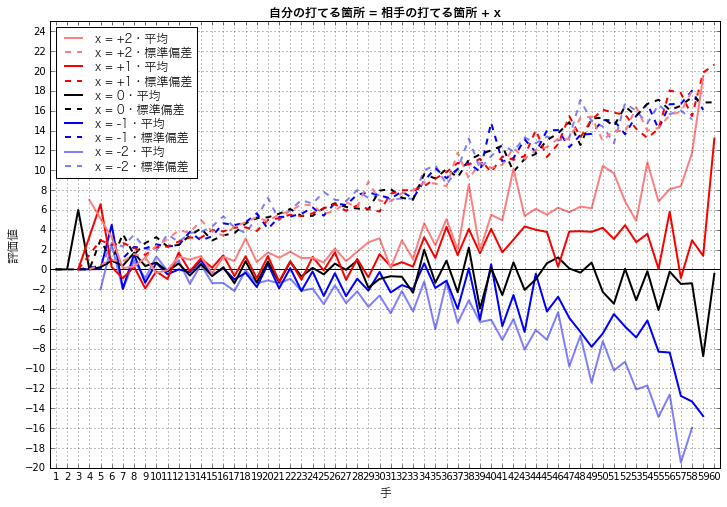xが自分と相手の打てる箇所の数の差を表しており、プラスが自分の方が多い局面(赤(+1)とピンク(+2))、マイナスが相手の方が多い局面(青(-1)と水色(-2))です。ゼロは自分と相手の打てる箇所が同じ局面でグラフでは黒の線で表しています。また、実線が平均値で点線が標準偏差です。

まず、自分の方が打てる箇所数が大きくなると(赤→黒→青)、予想通り評価値の平均は大きくなっています。そして中盤から終盤にかけてその上がり方も大きくなっています。つまり終盤の方が打てる1箇所あたりの価値が大きくなっているものと考えられます。

また、黒の線(差=0)を見ると序中盤は評価値0付近で推移していますが、終盤はややマイナス側に寄っているようです。赤の線(差=+1)を見ると終盤はややプラスですから、終盤は自分の方が打つ箇所数が多ければやや有利、等しい場合はやや不利くらいの状況のようです。

偶奇については交互に平均値が上下動しているようにも見えますが、各色とも連動している傾向があるようなので、打てる箇所の数の価値にはあまり影響がないのではないかと思われます。

標準偏差は色によらず終盤にかけて増え続けています。終盤に行くほど評価値の分布範囲が広がっているということなので、打てる箇所の数だけでは優劣が語れないということになります。ただし、そもそも評価値の分布は終盤に向かって広がっていくはずなので、終盤ほど打てる箇所の数の重要度が下がっているとは限らないように思われます。

試合の進行に対する打てる箇所1ヶ所あたりの価値を見たので、次は打てる箇所が多いか少ないかで、1ヶ所あたりの価値が変わるかどうかを見たいと思います。打てる箇所が少ない方が1つあたりの価値が高くなるのではないか、というのが予想です。

また、自分の打てる箇所と相手の打てる箇所の両方に関係してくるので、まずは相手の打てる箇所の数を固定して自分の打てる箇所の数によって優劣(評価値)がどう変わるかを見たいと思います。先ほど試合の進行による影響もありそうだったので、ここでは大雑把に序盤(1〜20手目)・中盤(21〜40手目)・終盤(41〜60手目)に分けて見ることにします。あまり細かく分けると情報量が多くなりすぎて見づらくなってしまうので。

ではまず試しに、相手の打てる箇所の数が11ヶ所の局面について、自分の打てる箇所数ごとに評価値を集計したグラフを見てみましょう。 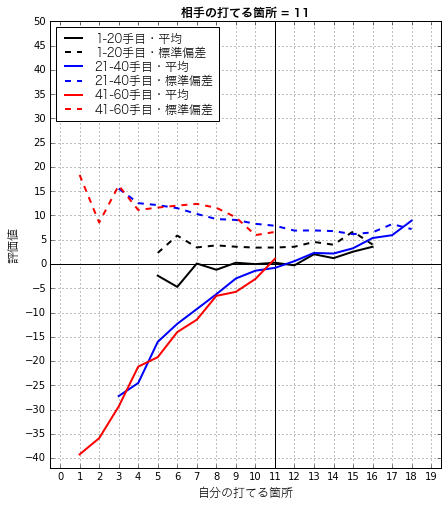黒が序盤、青が中盤、赤が終盤で、これまで同様に実線が平均、点線が標準偏差を表しています。このグラフの例えば自分の打てる箇所=9のところには、自分の打てる箇所が9ヶ所で相手の打てる箇所が11ヶ所の局面を序盤・中盤・終盤ごとに集めてきて平均と標準偏差をプロットしています。集めた結果該当する局面が10未満だった場合は、誤差が大きくなると思われるためグラフからは外しました。また、自分の打てる箇所数=11の軸が実線にしてあるのは、この線上が自分の打てる箇所数=相手の打てる箇所数なので、ほぼ互角に近いはずで、グラフを見る際に目安になると考えたためです。

グラフの内容ですが、序盤では自分の打てる箇所数は概ね5〜16の範囲に分布していて²⁾、自分の打てる箇所数が増えるにつれて緩やかに評価値が上昇しています。この傾斜が今回求めたい打てる箇所1ヶ所あたりの価値ですが、この場合は0.8前後でしょうか。標準偏差は4前後のようです。

中終盤については、中盤の方が打てる箇所数が多め、終盤は打てる箇所数が少なめの分布になっていますが、グラフとしてはだいたいつながっているように見えています。傾斜については打てる箇所数が多くなるにつれて徐々に緩やかになっているようにも見えますし、自分の打てる箇所数=9あたりで傾斜が変わっているようにも見えます。あとでもう少し詳しく見てみますが、打てる箇所数が少ないエリアでの傾斜は5くらい、多いエリアでの傾斜は1〜1.5くらいのようです。中終盤では試合が進んでいくと打てる箇所が徐々に少なくなっていきますから、先ほど見た終盤ほど打てる箇所1ヶ所あたりの価値が高いというのが現れています。標準偏差は自分の打てる箇所数が多くなるにつれて下がってきています。これも先ほど見た終盤ほど標準偏差が大きくなるというのが出てきているようです。

今見たのは相手の打てる箇所の数が11の局面だけを集めてきたものですが、相手の打てる箇所の数を変えながらグラフを作ってみます。以下がその結果です。 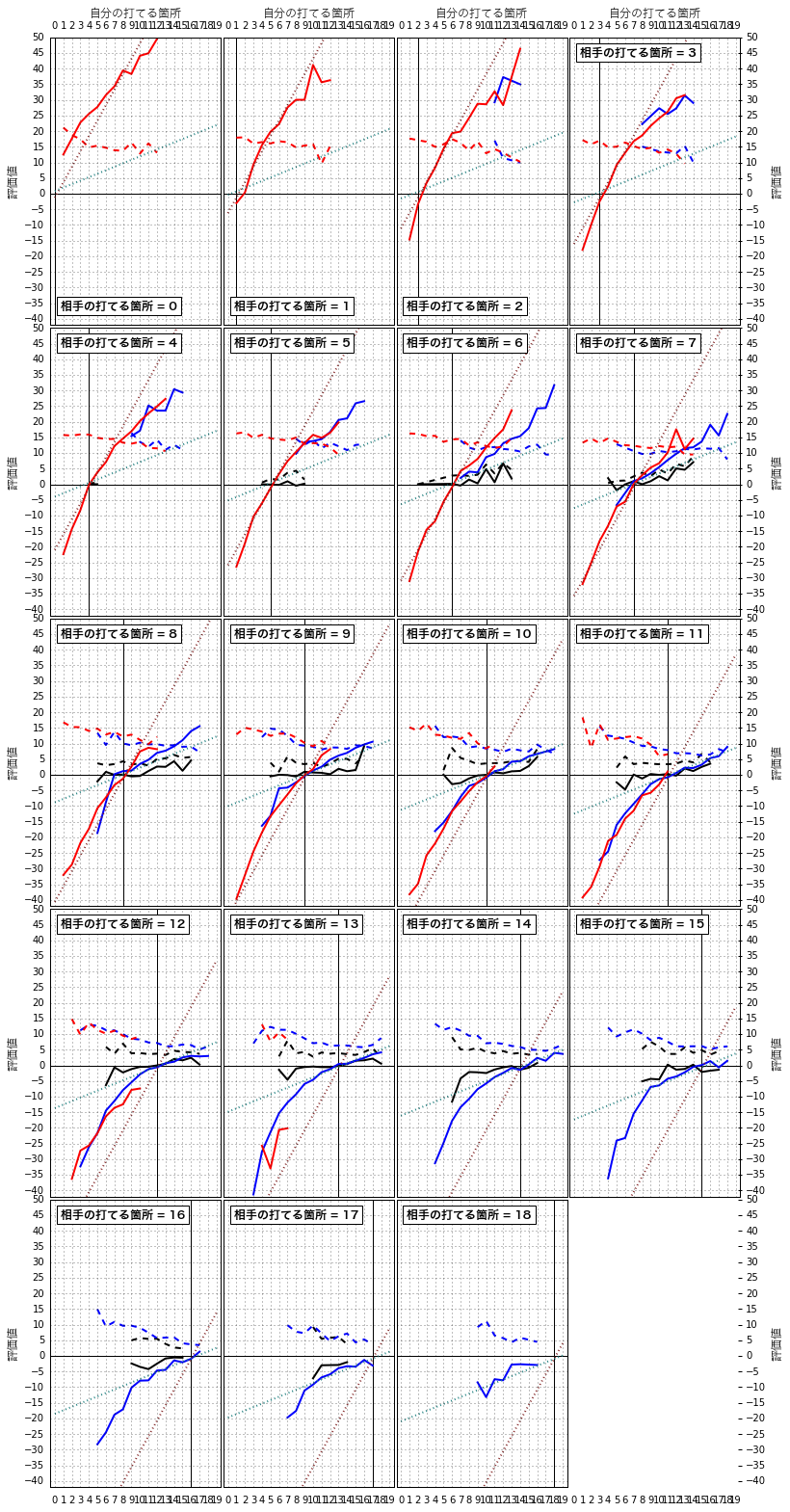見方は先ほどのグラフと同様です。斜めの点線が追加されていますが、あとで説明しますので今のところは無視してください。

序盤のグラフは相手の打てる箇所が4〜17の範囲に、中盤は3〜18の範囲に、終盤は0〜13の範囲に分布しています。先ほど同様、中盤と終盤の青と赤のグラフは概ねつながっているようです。序盤はいずれも緩やかな傾斜になっています。

グラフを眺めて気づくことは、中終盤(赤と青のグラフ)においてはやはり自分の打てる箇所数が少ない場合は1ヶ所あたりの価値が高く(傾斜が急)、増えるについれて価値が下がっていく(傾斜が緩やか)というところです。自分の打てる箇所数が8〜9あたりで傾斜が変わっているように見えるのも先ほどと同様です。そこで、中終盤(21手目以降)で自分と相手の打てる箇所数が8以下の時と9以上の時のそれぞれで、評価値の平均の回帰計算をしてみました。 $$score = 4.94m_p - 4.92m_o -1.28, (m_p\le8, m_o\le8)$$ $$score = 1.11m_p - 1.21m_o +0.85, (m_p\ge9, m_o\ge9)$$ $score$はもちろん評価値(の平均)で、$m_p$は自分の打てる箇所数、$m_o$は相手の打てる箇所数を表します。相関係数は上の式が0.96、下の式が0.94でした。グラフの斜めの点線の説明を先送りしていましたが、赤っぽい点線が上の式のグラフ、水色っぽい点線が下の式のグラフです。今見ている中終盤の赤と青の実線のグラフですが、赤の斜め点線は自分・相手の打てる箇所数が8以下の時に、水色の斜め点線は自分・相手の打てる箇所数が9以上の時に比較的よく当てはまっているように見えます。この式の$m_p$の係数がグラフの傾きですから、中終盤では自分の打てる箇所数が8以下だと1箇所あたりの価値は4.9石くらい、9以上だと1.1石くらいということになります。もちろん標準偏差が5〜15くらいですから、大半が$2\sigma$くらいの範囲に入るとしても評価値の誤差は10〜30くらいになり、打てる箇所の数だけでは推し量れないということも付け加えておきます。

序盤についてはどのグラフを見ても緩やかです。回帰計算もしてみましたが相関係数は0.67と思ったほど高くなりませんでした。一応結果は載せておきます。 $$score = 0.52m_p - 0.60m_o +0.84$$ 序盤は主に定石に基づいて打っているでしょうから、ほぼ互角の推移をすることが多く、打てる箇所の数と評価値が結び付きにくいのかもしれません。

あくまでも平均ベースの議論なので一概には言えませんが、目安として無理やりまとめます。

• 打てる箇所1ヶ所あたりの価値は、
  • 序盤は定石次第なので当てはまりにくいが、強いて言えば0.5石くらい
  • 中終盤で打てる箇所の数が多い間(9ヶ所以上)は、1.1石くらい
  • 中終盤で打てる箇所の数が少なくなる(8ヶ所以下)と、4.9石くらい
• 打てる箇所の数は20〜25手目付近が最大で、平均12ヶ所くらい
• 打てる箇所の数が自分=相手だと中盤くらいまではほぼ互角。終盤は自分が若干不利