手番の価値
手損って?
オセロの上級者と会話をすると、よく「手損」という言葉を耳にします。「手損」なので「手」を「損」するということですが、ちょっと直感と意味が違う言葉のように思います。
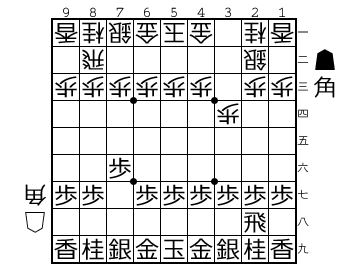 例えば将棋でも「手損」という言葉があります。将棋の場合は例えば序盤で▲7六歩△3四歩▲2二角成△同銀と進むと、お互い2手ずつ指して角を取り合ったことになります(右図)。この時、後手の駒は歩と銀が動いていますが、先手の駒はせっかく動かした角は取られてしまっているので実質的には歩1枚しか動いていないことになります。こういった状況が「手損」と呼ばれます。また、1手で行ける場所にわざわざ2手かけて移動しているようなケースも「手損」と呼ばれます。いずれにしても、将棋での「手損」はせっかくの手番を1回損してしまった、というニュアンスになります。
例えば将棋でも「手損」という言葉があります。将棋の場合は例えば序盤で▲7六歩△3四歩▲2二角成△同銀と進むと、お互い2手ずつ指して角を取り合ったことになります(右図)。この時、後手の駒は歩と銀が動いていますが、先手の駒はせっかく動かした角は取られてしまっているので実質的には歩1枚しか動いていないことになります。こういった状況が「手損」と呼ばれます。また、1手で行ける場所にわざわざ2手かけて移動しているようなケースも「手損」と呼ばれます。いずれにしても、将棋での「手損」はせっかくの手番を1回損してしまった、というニュアンスになります。
ではオセロの場合はどうでしょう?Othello! JAPANの初心者向け講座のページに手損の説明がありますが、将棋と違って、手数をかけた分だけ盤面にその影響を残した(平たく言えば、自分の色を増やした)方が「手損」ということになっています。また1回で裏返せる石たちをわざわざ2回かけて返すのは、「手損」ではなく「手得」になります。
ざっくりと(雑に)まとめると以下のような感じです。
| 状況 | 将棋 | オセロ |
|---|---|---|
| 自分と相手で同じ手数をかけて、盤上自分の駒がたくさん動いた(自分の石がたくさん増えた) | 手得 | 手損 |
| 1手でできることに2手かけた | 手損 | 手得 |
| 下記の2つの手順で結果的にほぼ類似の局面になる (A)自分→相手の2手 (B)自分→相手→自分の3手 | (A) 手得 (B) 手損 | (A) 手損 (B) 手得 |
オセロの場合は手番を損したというわけではなく、打てる場所(手数)を無駄に減らしてしまったということを「手損」と呼んでいるようです。どちらかと言えば、手番は損をした(たくさん消費した)方が「手得」ということになります。つまり、オセロのこの常識は「手番」を持っていることはマイナスに作用することが多いということを言っていることになります。
手番の価値を考える
オセロや将棋において「手番」の価値というのは、その局面で一番良い手を打つ権利を持っているという価値です。もしオセロの手番の価値が本当にマイナスなのであれば、その局面で一番良い手ですらマイナスの価値しかない、ということになるはずです。確かにオセロではほとんどの場合、手を打つということは自分の打てる場所を減らしてしまうというマイナスの作用があります。しかし手を打つことには確定石を増やすとかプラスの作用もあるはずです。このプラスマイナスを合わせたものがその手の価値になるはずですが、両方合わせても本当にマイナスなのか、本当だとしたらどの程度マイナスなのかということを調べてみたいと思いました。
算出方法
オセロの解析ソフトを使うと、手の評価値を出すことができます。今知りたいのは「手番」の価値ですが、ある局面で最善の手の評価値が例えば+3だったとして、「手番」に+3の価値があるというわけではありません。なぜなら、その局面の形勢はすでに+3であって、最善手はその形勢を維持するという効果はあるにせよそれ自体に+3上積みする効果があるわけではないからです。「手番」の価値が知りたいのですから、
- 「手番」を持っている場合の形勢(=最善手の評価値)
- 「手番」を持っていない場合の形勢(=最善手の評価値)
を比較すると良いはずです。例えば黒番のある局面で形勢(最善手の評価値)が+3だったとします。もし仮に全く同じ盤面で黒が手番を失ったら形勢はどうなるか、と考えるのです。言い換えると本来黒はパスできないはずですが仮に黒がパスして手番を相手に譲ったら形勢がどうなるか、ということです。このとき、白から見て形勢が-3だったとしたら、形勢は全く変わっていない、すなわち手番の価値は0ということになります(最初の+3は黒から見ての形勢なので、白から見て-3なら形勢が変わっていないという意味になります)。
もし白から見たときの形勢が-1になっているとしたら、白にとって形勢は2改善したことになります。黒から見ると2悪化したことになりますから、その局面で手番の価値は差し引き+2だった(手番を放棄すると2損してしまうので)ということです。
逆に白から見たときの形勢が-5になっているとしたら、白にとって形勢は2悪化したということです。黒から見るとその局面での手番の価値は差し引き-2(手番を放棄したら2得したので)ということになります。
ある局面Aにおける手番の価値を計算式で表すと以下の通りです。
= 局面Aでの最善手の自分から見た評価値 + 局面Aが相手番だとした場合の最善手の相手から見た評価値
結果
実際に棋譜を集めて手番の価値がどの程度なのかを計算してみました。棋譜はフランスオセロ連盟のWTHORファイルがあったのでこれを使うことにしました。2017年9月現在、全部で12万局以上の棋譜があったのですが、さすがに多すぎるのでこの中の全日本選手権の棋譜1035件に絞りました。解析はEdaxのレベル18で行いました。私のパソコンで約3日かかりました…。
全体の分布
約1000局×60手分なので約6万局面あるわけですが、その6万局面の手番の価値の分布を現したのが以下のグラフです。
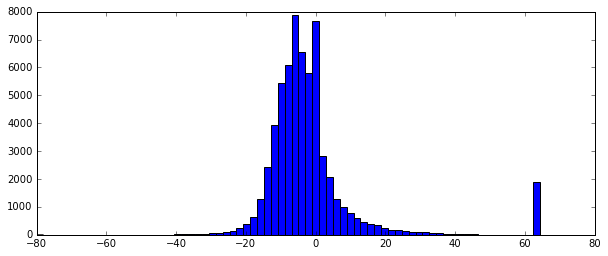 マイナスの値を中心に分布しているように見えはしますが、0付近と-6付近の2つピークがあるように見えますし、+64付近と思われるところに謎の山ができています。
マイナスの値を中心に分布しているように見えはしますが、0付近と-6付近の2つピークがあるように見えますし、+64付近と思われるところに謎の山ができています。
手番ごとの分布
6万局面分一気にグラフにしたせいで何かの特徴を見失っているように見えるので、試しに23手目と24手目に絞ったグラフも作ってみました。
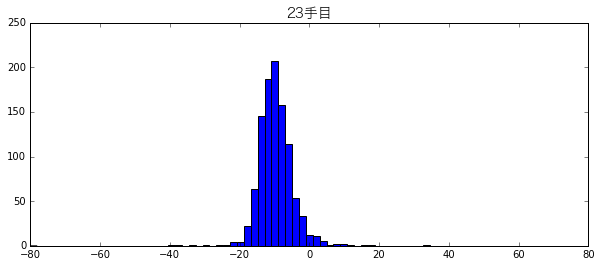
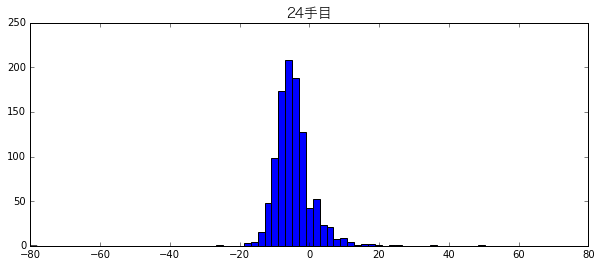 先程よりはきれいなグラフになっています。23手目の方が24手目よりも若干左側にピークがあるようです。そして+64付近の謎の山もありません。どうやら手番(今何手目なのか)でグラフを分けた方が良さそうです。ただ、60個のグラフを並べるのも見づらいので、「箱ヒゲ図」というグラフで1手目から60手目までの手番の価値の状況を描いてみることにします。
先程よりはきれいなグラフになっています。23手目の方が24手目よりも若干左側にピークがあるようです。そして+64付近の謎の山もありません。どうやら手番(今何手目なのか)でグラフを分けた方が良さそうです。ただ、60個のグラフを並べるのも見づらいので、「箱ヒゲ図」というグラフで1手目から60手目までの手番の価値の状況を描いてみることにします。
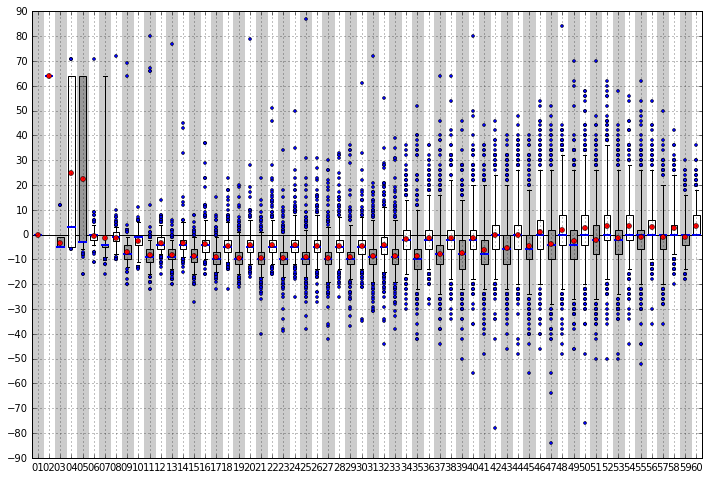
簡単に言えば、箱の範囲に全体の50%のデータがあり、ヒゲの範囲に全体の95%のデータがあるということです。
なおグレーと白の着色は見やすさのためです。
例えば1手目はどこに打っても評価値0で、手番を白に譲っても同じく評価値0なので、手番の価値は必ず0になります。グラフ上も全て0になっています。2手目は白番で、縦取りか斜め取りをすれば評価値0ですが、手番を黒に譲ってしまうと白は全滅してしまうので黒の評価値は+64、手番の価値はグラフでもわかるように+64です。つまり手番に+64の価値があって譲ると損をするということです。これが先ほど+64付近に見えていた謎の山の正体のようですね。
グラフを見ると10手目くらいまでは荒い動きがありますが、その後は比較的落ち着いた動きになっています。そして一目見てわかるように価値の値が1手ごとにジグザグに動いています。全体的にグレーで着色した奇数手目の手番の価値よりも、白い偶数手目の手番の価値の方が高いようです。ちょっと考えてみると、偶数理論が生かせる最終手を打てるのは偶数手番側(通常白)ですから、奇数側はどちらかと言えば手番を譲りたい(手番の価値が相対的に低い)、偶数側はどちらかと言えば手番を譲りたくない(手番の価値が相対的に高い)わけです。
グラフが細かすぎて値が見づらいので、奇数手目と偶数手目に分け、さらに序盤の10手を削ってもう少し拡大して詳しく見てみることにしましょう。
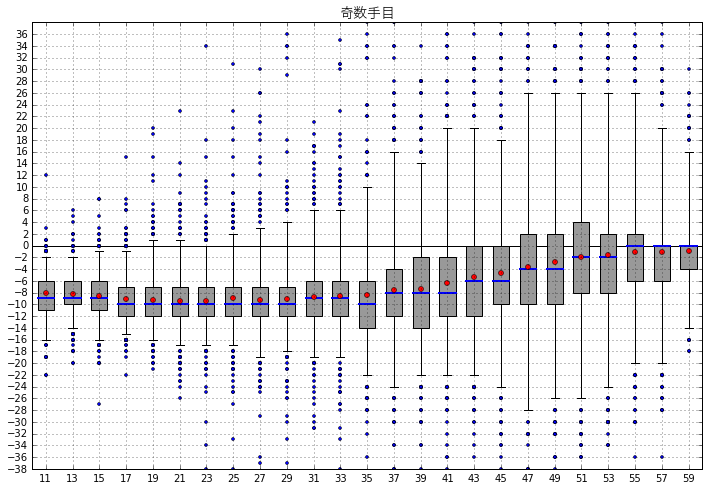
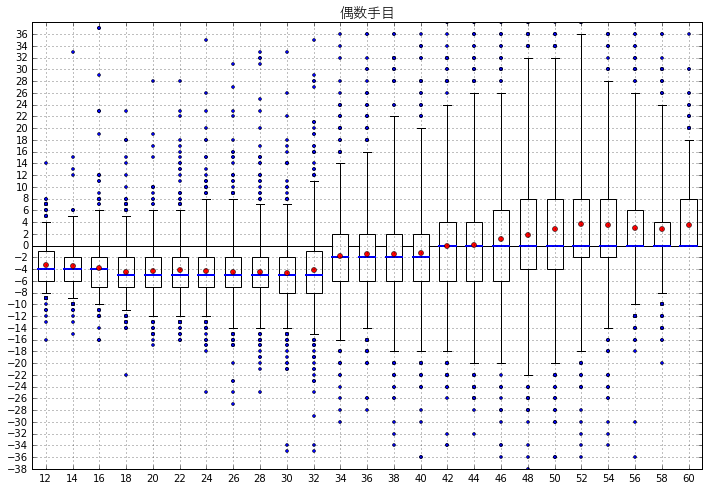 大分きれいになりました。いろいろと気づくことがありますね。
大分きれいになりました。いろいろと気づくことがありますね。
- 30手目過ぎまで
- 奇数手目は-8〜-10あたりを中心に推移
- 偶数手目は-3〜-5あたりを中心に推移
- 30手目過ぎ以降
- 中央値・平均値が上がり始め、奇数・偶数とも最終的には0が中央値になる。ただし分布は奇数手目についてはマイナス方向に、偶数手目についてはプラス方向に偏っている
- 分布の範囲(箱やヒゲの長さ)が広がり始める。50手目くらいまで、ヒゲの上端は上昇傾向、下端は下降傾向にある
また、元々は手番の差し引きの価値がプラスなのかマイナスなのかを見ようとしていたので、その観点でもグラフ化しておきます。下のグラフは手番の価値が「プラス」「ゼロ」「マイナス」の局面の比率を手番ごとに表したものです。
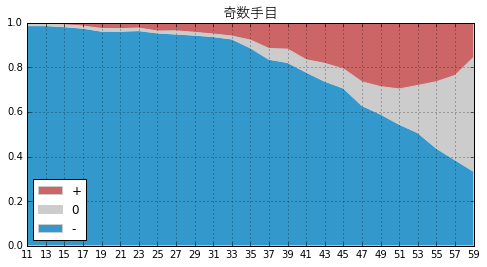
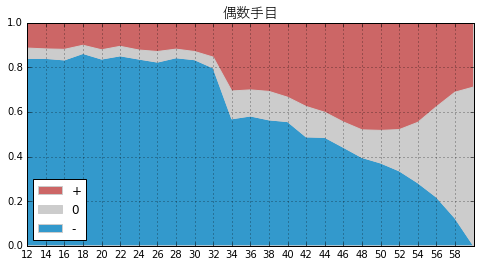
- 奇数手目はだいたいマイナスが多い。プラスは多くても3割くらい
- 偶数手目も中盤くらいまではマイナスが多いが、最終盤はプラスが多い
箱ヒゲ図も比率のグラフもそうですが、偶数手目のグラフで32手目と34手目の間で急な変化が見えますが、ここにはオセロの性質とは別の原因が潜んでいる可能性があります。今回の計算は先ほども書いたようにEdaxのレベル18で行っているのですが、レベル18では33手目までは深さ18の読みなのに対して、34手目以降は最終手まで読んでいます。不連続的な変化の原因は、この読みの深さの違いの可能性が高いように思います。値の信憑性は最終手まで読んでいる34手目以降の方が高いですから、本当は32手目以前の手番の価値はもう少し高い(プラスの比率がもう少し多い)可能性がありそうです。ただし、奇数手目においては33〜35手目の間でそれほど顕著な差はないように見えるので、どういうことが起こっているのか実際のところはよくわかりませんでした。なので、特に32手目以前の偶数の価値は少し不正確な可能性があることを頭の隅に置きつつ話を進めたいと思います。
考察
さて、グラフからの気づきが何を意味するのか考えてみましょう。
まず、奇数手目と偶数手目の差が中盤くらいまではおよそ5くらいあります。先ほど考えたように、これは偶数理論の効果と考えられます。奇数手目と偶数手目(例えば11手目と12手目)の価値の平均値の差もグラフにしてみました。
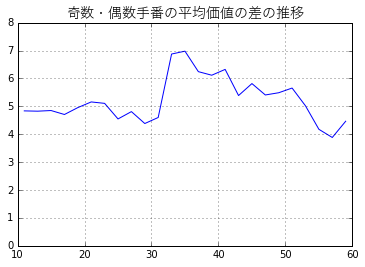 偶数理論の生かせる偶数手番の方が差し引き4〜7石分くらい有利なようです。ちょっと疑問なのは、偶数空き1箇所で後手番はこれくらい得をしそうな気がするので(私の棋力的に感覚が正しくないかもしれませんが、もし感覚がおかしければコメント欄でご指摘ください)、終盤に偶数空きが複数箇所できればもっと得が大きくなるような気もします。しかし、逆偶数になったりハイパー偶数があったりする場合など偶数理論が働かないケースもあるので、おそらく平均化すると4〜7石くらいということなのだろうと思います。元々は手番の価値を調べようとしていましたが、副産物として偶数理論の効果を見ることができました。
偶数理論の生かせる偶数手番の方が差し引き4〜7石分くらい有利なようです。ちょっと疑問なのは、偶数空き1箇所で後手番はこれくらい得をしそうな気がするので(私の棋力的に感覚が正しくないかもしれませんが、もし感覚がおかしければコメント欄でご指摘ください)、終盤に偶数空きが複数箇所できればもっと得が大きくなるような気もします。しかし、逆偶数になったりハイパー偶数があったりする場合など偶数理論が働かないケースもあるので、おそらく平均化すると4〜7石くらいということなのだろうと思います。元々は手番の価値を調べようとしていましたが、副産物として偶数理論の効果を見ることができました。
では元々の問題だった手番の価値について考えてみます。今回の計算は仮にパスが発生したらという仮定で行いました。実際のオセロでは「手損」したとしてもパスになるわけではないので最終手を打つ権利は移動しません。なので実質的な手番の価値は、この偶数理論の効果を除いて考えた方が良さそうです。そこで奇数手番と偶数手番を平均化してみると、30手目過ぎまでは-6〜-7石くらいが実質的な価値ということになります。マイナスの値ですから、オセロではやはり「手損」という言葉の示唆通り、手番は持っていない方が良いことが多いということが言えそうです。
終盤に入ってくると、分布の範囲が広がってきていますが、これは手番を持っていた方が良いようなケースがあったり、盤面が詰んでいてどこに打ってもひどい状況になっているケースがあったりと、要するにケースバイケースで「一概には言えない」ということのようです。無理矢理平均化すると、40手目台はややマイナス、50手目台はややプラスといったところでしょうか。
今回のところは「手番の価値」ということで、「手番」そのものがどの程度の価値を持っているかをいろいろと調べてみました。しかし調べているうちに、オセロの「手損」を理解するためには「打てる場所の数」にどの程度の価値があるかも合わせて見る必要がありそうに感じました。これはまた別の機会に調べてみたいと思います(機会があれば…)
結論
- 手番の価値は中盤は-6〜-7石くらい
- 終盤は平均的には0に近づくが、局面による差が大きい
- 終盤の偶数手番側の有利さ(偶数理論の平均的な効果)は4〜7石くらい