%の意味
Edaxを使い始めて、最初に面食らったのがこんな表示でした。
depth|score| time | nodes (N) | N/s | principal variation ------+-----+--------------+-------------+----------+---------------------- 21@73% +05 0:19.104 109196286 5715886 B4 a5 F7 c6 E1 d1 C1 g5 H6 21@73% +04 0:00.103 284886 2765883 F7 b4 E1 g6 C6 a6 D1 f8 G5 21@73% +01 0:00.012 40353 3362750 E1 d1 F7 f2 F1 g3 C6 g1 B1 ------+-----+--------------+-------------+----------+----------------------
最初のdepthとかいてある部分の意味がわかりませんでした。まぁ、depthなので読みの深さだというのはわかりますし、21がその深さを表しているのだろうというのも良いのですが、「@73%」と何の説明もなく出てくるのが理解できなかったわけです。
この意味は結局ソースコードを見て初めてわかりました。前回のレベルの意味でも少し触れましたが、この%の値はselectivity(選択性?)というものでした。今回は、このselectivityについてもう少し詳しく調べてみたいと思います。
Edaxの評価値の出し方
前回の復習
レベルの意味でも書きましたが、Edaxは評価値を出す際に、
- 0手読みの評価値
- 先読み評価値
を基本としていました。0手読みというのは盤面だけを見て算出する値、先読み評価値というのはある深さまでを網羅的に読んだ時の末端の局面の「0手読み評価値」の中で両者最善を打った場合の評価値でした。そして、この先読み評価値を網羅的に調べるのは時間がかかりすぎるので、Edaxは「うまくサボる」ということを前回書きました。今回はこのサボり方について、もう少し詳しく調べてみます。
アルゴリズムのイメージ
下の図のような状況を考えます。一番上が現在の局面で、打てる手がa,b,cの3箇所あり、aを打ったら局面Aに、bを打ったら局面Bに、cを打ったら局面Cになります。これらの局面A〜Cでも相手の打てる手が3箇所ずつあり、打った先が一番下に並んでいる9つの局面になります。
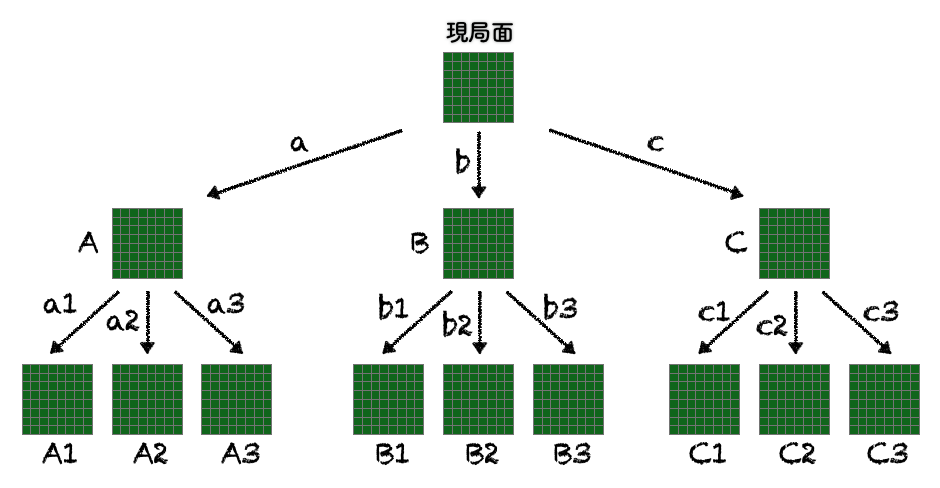 この状況で、現局面における2手先まで読んだ評価値を考えてみたいと思います。対局者はXさんとYさん、現在の局面(一番上の局面)の手番はXさんとします。
この状況で、現局面における2手先まで読んだ評価値を考えてみたいと思います。対局者はXさんとYさん、現在の局面(一番上の局面)の手番はXさんとします。
手aについて考える
Xさんが手aを打つと局面Aになります。局面Aで可能なa1〜a3をYさんが打った局面A1〜A3について、Xさんから見た「0手読み評価値」を算出したところ、それぞれ+4,+2,+9だったとしましょう。Yさんは最善、つまりXさんから見た評価値がなるべく低くなるように打ちますから、局面Aでは手a2を選ぶことになります。なので、局面AにおけるXさんから見た評価値は+2です(Yさんから見ると-2です)。この評価値は、局面Aで1手先読みした評価値になります。
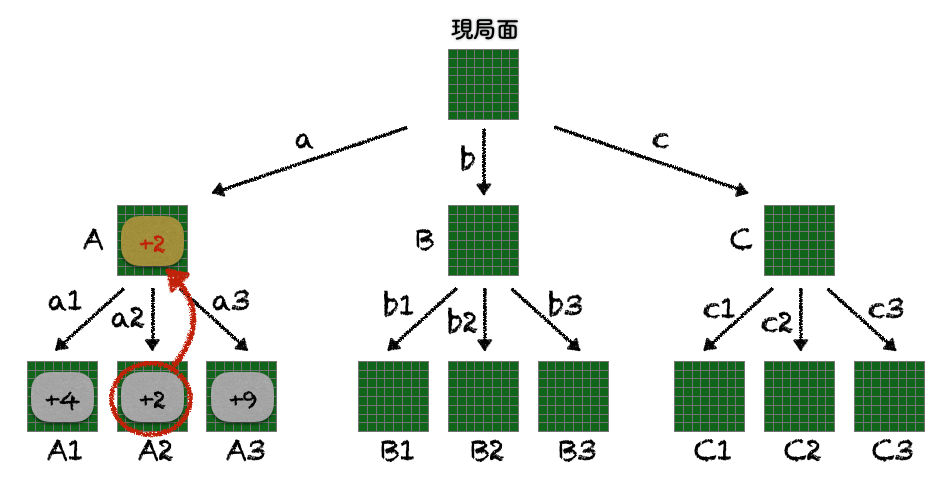
手bについて考える(結果に影響しないサボり方の例)
前回、Edaxの計算のサボり方には結果に影響しないサボり方と、結果に影響するサボり方があると書きました。手bで「結果に影響しないサボり方」について見てみたいと思います。
手bを打った局面Bで可能な手も3通りありますが、まずは手b1の先の局面B1について「0手読み評価値」を算出してみたところ、Xさんから見て-1だったとしましょう。まだb2とb3については調べていませんが、Yさんはb1を選べばXさんから見た評価値を-1にすることができます。仮に、局面B2やB3の0手読み評価値がもっと大きい値(例えば+5とか)だったとしても、Yさんはb1を選べば良いですから、局面BにおけるXさんから見た評価値は-1より大きくなることはないことがわかります。先ほど、手aで局面Aの評価値がXさんから見て+2だったことが既にわかっていますから、評価値が-1より大きくなることのない手bはXさんにとって悪い選択にしかならないことがこの時点で確定しています。もしB2やB3の評価値がもっと小さい値(例えば-5とか)だったらYさんはそちらを選ぶことになりますが、Xさんにとってはさらに悪い結果になるだけで、手bを選ぶ理由はなおさらなくなります。つまり、局面B1の0手読み評価値の結果によって、局面B2やB3を調べなくてもXさんにとって手bが最善であることはありえないことが確定しています。これが結果に影響しないサボり方です。
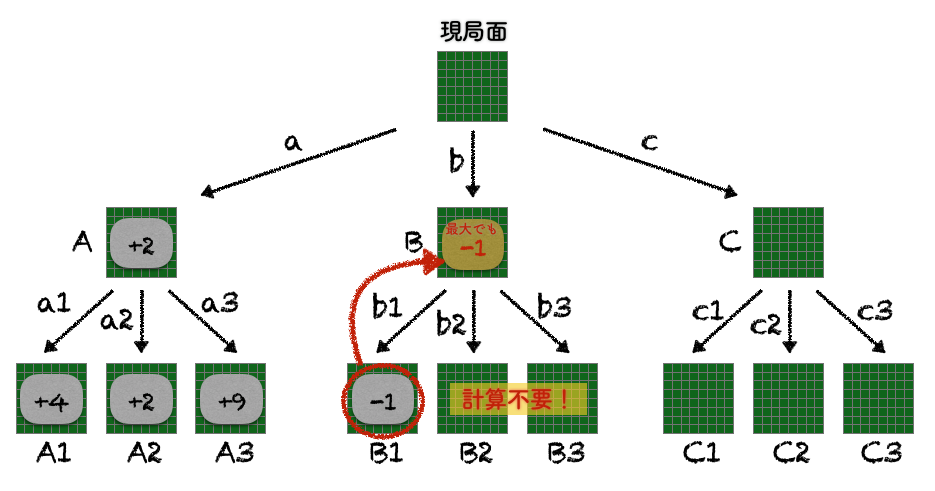
手cについて考える(結果に影響するサボり方の例)
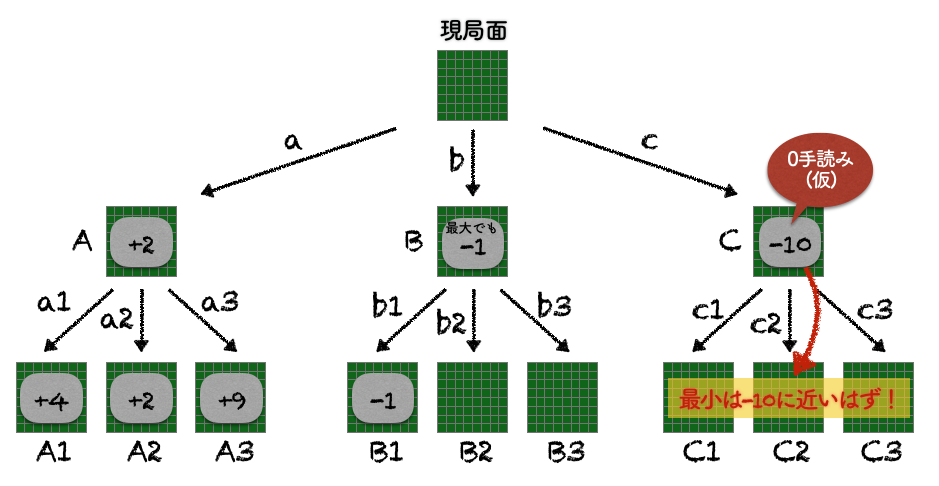
手cで「結果に影響するサボり方」の例を見てみます。先ほどの手bでは、分岐の1つだけではありますが先読みを行って判断を行いました。しかし手cが「まずこんな手はあり得ないよね」みたいなひどい手であれば、分岐の1つだけですら先読みするのがもったいないので、分岐を1つも読まずに手cを却下したいところです。Edaxではこの「ひどい手」かどうかを判断するのに局面Cにおける「0手読み評価値」を使います。仮に局面CにおけるXさんから見た「0手読み評価値」が-10だったとしましょう。この-10という値は先読みせずに行っていますが、精度は不十分だとしても「ある程度」は正しい値のはずです。つまりYさんが手c1〜c3の中の最善の手を選べば、その先の局面C1〜C3のどれかは-10に「ある程度」近い値になるはずです。この値が手aの+2を上回らなければ手cを却下することができます。
厳密にソースコードを追いきれてはいないのですが、Edaxではこの「ある程度近いはず」という判断を-10を平均とした正規分布と仮定しているようです。そしてその標準偏差は局面Cと末端局面(C1〜C3)の深さの差(今の例では1手ですが)や残りの空きマス数から算出できる値だとしています。この仮定の下で、局面C1〜C3の評価値の最小値が+2よりも小さくなる確率を求めて、その確率が十分に大きければ手cを却下する、という考え方をしています。この却下するかどうかの確率の判断基準がselectivityで、Edaxで読みを行うとよく表示される73%、87%、95%、98%、99%、100%という値がそのパーセンテージになっています。selectivity=73%で読みを行う場合、標準偏差から判断してC1〜C3の評価値が+2以下になる確率が73%以上であれば、手cを却下します。この73%、87%、95%、98%、99%の値は、$\sigma$を標準偏差として、$1.1\sigma, 1.5\sigma, 2.0\sigma, 2.6\sigma, 3.3\sigma$以内に入る確率になっています。Edaxのプログラム内の評価ではパーセントの値ではなく、この$\sigma$の係数を使って却下するかどうかを判断しています。
 Edaxのソースを見ると、本当はもっと複雑なことをしていて、Cのような局面で0手読み評価値を出してみて、却下できそうな見込みがあれば残りの深さの半分くらいまで先読みしてみて、それでも却下できるという判断に至れば却下する、というようなことをしているようです。この手法はProbCutと呼ばれているようで、Logistelloで採用されたのが最初だそうです。
Edaxのソースを見ると、本当はもっと複雑なことをしていて、Cのような局面で0手読み評価値を出してみて、却下できそうな見込みがあれば残りの深さの半分くらいまで先読みしてみて、それでも却下できるという判断に至れば却下する、というようなことをしているようです。この手法はProbCutと呼ばれているようで、Logistelloで採用されたのが最初だそうです。
確率で判断していますから絶対正しいという保証はありません。なので、結果に影響するサボり方という言い方をしました。結果に影響するとは言ってもある程度は正しいはずで、その誤差がどれくらいになるのかは後で調べてみたいと思います。
結局評価値は・・・
ここまでの計算によって、手aは+2、手bは最大でも-1、手cは-10くらい(あるselectivityの値で+2を超えないと判断)ということになりましたから、元々の局面における評価値は最善手であるaを打った時の+2であるということになります。
上記で説明した例は2階層くらいまでしかなかったので、計算を省略すると言っても大した効果がないようにも見えますが、もっと深い読みでの評価値を出そうとしている場合は省略することのできる局面数も多くなります。Edaxでは多少精度が悪くなっても、実用的な時間内で計算できるように工夫しているということになります。
時間短縮効果と精度への影響
すでに記事がだいぶ長くなってしまいましたが、実はここまでは前置きです。先ほど書いたように今回知りたかったのは、selectivityによる計算の省略を行った結果どれくらいの時間が短縮できて、それによってどの程度評価値の精度が悪くなっているのか、ということです。73%以上の確率でそれまで調べた最善を超えないことがわかったと言っても、そういう省略を何度も何度も行っていたら結構な確率で最善を超えるような分岐を読み落としている可能性があるのではないかという疑いがあります。今回はこれを調べてみたいと思います。
実験を行う前に
今回もWTHORの中から全日本選手権の棋譜1035件を使って実験してみることにします。実験の前に、どういうことを想定して実験を行うべきか考えてみました。
- 当然のことながら、selectivityの値が小さい方が精度が悪いはず。selectivityの値による精度の影響を知りたい。
- 読みの深さによっても精度の違いが出てくるかもしれない。読みの深さによってProbCutの影響度合いが変わるのかも知りたい。
- 序盤なのか中盤なのかによっても精度の違いが出てくるかもしれない。何手目かによってProbCutの影響度合いが変わるのかも知りたい。もしかしたら偶数手目と奇数手目で影響が違うかもしれない。
これらを念頭に置いて、以下の条件で計算をしてみることにします。
- 1つの棋譜から、6〜40手目の中から5手ずつを計算対象として抽出(例えば、ある棋譜からは7,14,21,28,35手目、別の棋譜からは9,16,23,30,37手目のように7手おきに抽出しました。また6〜40手目までがほぼ均等になるように抽出しました)
- 抽出した局面に対し、深さ6〜15までの10パターン、selectivityは73%、87%、95%、98%、99%、100%の6パターン、計10*6=60パターンの条件で評価値を算出
この計算により、selectivity = 73%、87%、95%、98%、99%の各パターンを、同じ局面・深さにおけるselectivity = 100%(ProbCutしない)と比較すれば、各局面の読みでProbCutによってどれくらい評価値がずれたかがわかります。
6手目以降にしたのは、5手目くらいまでは棋譜のバリエーションも限られているでしょうし、ほとんどの場合はbookに登録されていてselectivityの影響を調べても実用上あまり役に立たないと思われるからです。41手目以降を調べなかったのは、レベルの意味でも書いた通りEdaxはselectivity=100%の完全読みをするのでやはりselectivityの影響を調べても役に立たないからです(本当は40手目も役に立たないですね。既に計算してしまったので、せっかくなので40手目は結果を後で載せます)。
深さは6からにしていますが、実は深さ5以下も実験はしてみたのですが、ProbCutが行われなかったため除外しました。深さ15までなのは計算時間の都合上です。
では実験を、と行きたいところですが、残念ながらEdaxではレベルの設定により深さとselectivityを変えることはできても、それらは連動しているので、深さとselectivityを独立して設定することはできません。そこで何手目にどの深さでどのselectivityで読みを行うかを外部から指定できるよう、Edaxを改造して実験を行いました。
所要時間の結果
では結果です(計算し始めてから3日半かかりました・・・)。
ややこしそうな評価値の精度は後回しにして、まずはselectivityによって計算時間がどれくらい変わったかを見てみます。参考までに実行環境は以下の通りです。
- 機種:MacBook Air
- CPU:Intel Core i7 1.7GHz, 2コア
- メモリ:8GB
ではまず深さ6の計算時間から。
 横軸が何手目かを表しますが、6〜12手目、13〜19手目のように7手ずつ区間分けして、区間ごとに平均を取っています。selectivityごとに折れ線グラフを描いています。selectivityを変えても、大して計算時間の短縮にはなっていないようです。しかも99%が割と速かったり、変な結果です。浅めの読みでそもそも10msくらいしかかかっていないので、目に見える効果はないようです。
横軸が何手目かを表しますが、6〜12手目、13〜19手目のように7手ずつ区間分けして、区間ごとに平均を取っています。selectivityごとに折れ線グラフを描いています。selectivityを変えても、大して計算時間の短縮にはなっていないようです。しかも99%が割と速かったり、変な結果です。浅めの読みでそもそも10msくらいしかかかっていないので、目に見える効果はないようです。
続いて深さ10の場合を見てみます。
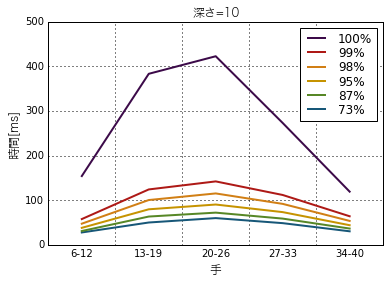 差が見えるようになってきました。と言っても一番時間がかかる20〜26手目あたりでもselectivity=100%で400ms強なので実用的にはあまり差はないですが、100%と73%を比べると10分の1近くに所要時間が短縮できているようです。99%と73%を比べると半分くらいでしょうか。
差が見えるようになってきました。と言っても一番時間がかかる20〜26手目あたりでもselectivity=100%で400ms強なので実用的にはあまり差はないですが、100%と73%を比べると10分の1近くに所要時間が短縮できているようです。99%と73%を比べると半分くらいでしょうか。
最後に深さ15の場合です。
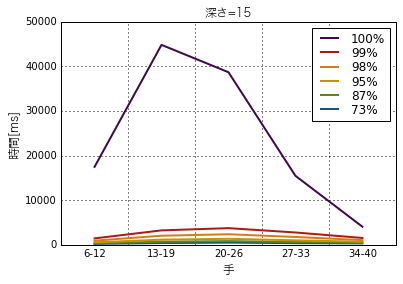 これはProbCutの威力を発揮していますね。深さ15ではピークが少し前寄りにシフトして、13〜19手目あたりになっていますが、selectivity100%と99%の間でも10分の1以上の短縮になっています。その下はグラフ的には潰れてあまりよく見えませんが、調べてみると99%と73%の間でも10分の1近い短縮がありました。100%と73%では100分の1くらいの短縮効果があるようです。
これはProbCutの威力を発揮していますね。深さ15ではピークが少し前寄りにシフトして、13〜19手目あたりになっていますが、selectivity100%と99%の間でも10分の1以上の短縮になっています。その下はグラフ的には潰れてあまりよく見えませんが、調べてみると99%と73%の間でも10分の1近い短縮がありました。100%と73%では100分の1くらいの短縮効果があるようです。
ここまでの状況から、読みの深さが深くなるほどProbCutによる時間短縮効果は大きくなると言えそうです。もちろん読みが深いほど計算する必要のある分岐数は増えますから、絶対値として速くなるというのもありますが、短縮の比率も大きくなってきています。
評価値精度の結果
では本題の評価値の精度について見てみたいと思います。今回はselectivityが精度をどれだけ悪くしているのかを知りたいので、例えば深さ10・selectivity87%で探索した結果の評価値であれば、同じ局面で深さ10・selectivity100%で探索した評価値と比較して、どれだけ値が変わってしまったか(誤差)を見ることにします。
深さ15・selectivity73%の場合
全体像をいきなり捉えるのは難しそうなので、まず、一番誤差が大きくなりそうな深さ15・selectivity73%の探索結果について、1035局×5手(各局、6手目〜40手目の中から5手ずつ抽出しているので)の約5000局面の誤差の分布を見てみます。
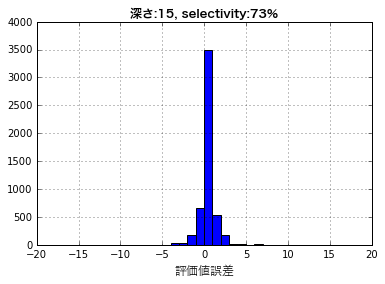 半分以上は誤差0になっていて、±2の範囲にほとんど収まっているようです。73%という基準で深読みするかどうかの判断をしているので、もっと誤差が大きくなるのかと思っていたのですが、思いの外誤差が小さいようです。ただ、グラフ上誤差は-4〜+6の範囲に見えますが、実は肉眼(?)で見えないだけで最小で-20、最大で+12の誤差が出た局面もありました。数は少ないながら大きな誤差が出る局面もあるようです。
半分以上は誤差0になっていて、±2の範囲にほとんど収まっているようです。73%という基準で深読みするかどうかの判断をしているので、もっと誤差が大きくなるのかと思っていたのですが、思いの外誤差が小さいようです。ただ、グラフ上誤差は-4〜+6の範囲に見えますが、実は肉眼(?)で見えないだけで最小で-20、最大で+12の誤差が出た局面もありました。数は少ないながら大きな誤差が出る局面もあるようです。
分布の範囲がわかったので、その局面が何手目かによって誤差がどう変わるのかについても見てみたいと思います。以前も使った箱ヒゲ図で見てみたいと思います。
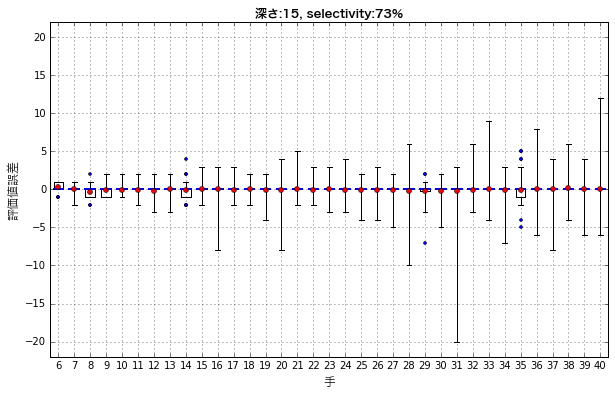
簡単に言えば、箱の範囲に全体の50%のデータがあり、ヒゲの範囲に全体の95%のデータがあるということです。
グラフを作っては見たのですが、箱はほとんどつぶれていて残念な感じです。箱がつぶれているということは、全体の50%以上が誤差=0だということを表します。平均値や中央値もほぼ0になっています。ヒゲが表す95%のデータの分布範囲は、広くなったり狭くなったり不安定ですが、これは1手あたり150局面くらいずつと、サンプル数が少なめであるためと思われます。細かい動きは無視すると、全体的には手が進むにつれて広がってきているように見えます。今回は、以前の手番の価値を見たときのように、偶数手と奇数手で顕著な傾向があるようには見えません。
さて、箱ヒゲ図では25%〜75%の範囲と2.5%〜97.5%の範囲しか見えず、分布の傾向が今ひとつわかりにくいので、もう少し細かく区切って見てみたいと思います。細かく区切ると箱とヒゲだけでは表現できないので、色で表してみることにします。
また、手毎の分布については細かい傾向よりは全体傾向を見たいので、先ほどの計算時間の時と同様に6手目〜12手目、13手目〜19手目、…と7手ずつまとめて見ることにします。以下が作ってみたグラフです。
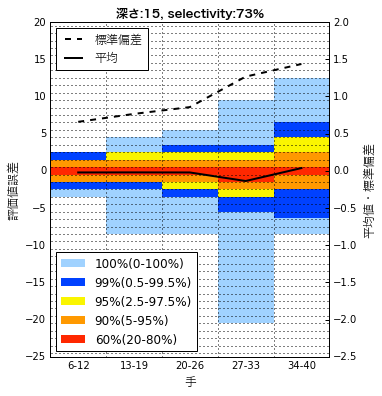 見るのに慣れが必要なグラフになってしまいましたが、先ほどより雰囲気がつかみやすくなりました。一般的な形式ではないので、まずはグラフの見方を説明します。
見るのに慣れが必要なグラフになってしまいましたが、先ほどより雰囲気がつかみやすくなりました。一般的な形式ではないので、まずはグラフの見方を説明します。
横軸は何手目かを表します。7手ずつまとめているので、一番左側のエリアが6手目〜12手目、一番右は34手目〜40手目になっています。縦軸(左側の軸)は評価値の誤差で、selectivity=100%で探索した時と比べてどれくらいずれたかを表します。プラスの場合はselectivity=100%と比べて+の方向に誤差が出たもの(つまり楽観的な読みになったもの)を表します。色は全体の何%がそこに分布しているかを表します。例えば27手目〜33手目の部分で見ると、以下のような分布になっています。
- 全体の60%以上(赤)は誤差-1〜0の範囲に分布
- 全体の90%以上(オレンジ)は誤差-2〜+1の範囲に分布
- 全体の95%以上(黄)は誤差-3〜+2の範囲に分布
- 全体の99%以上(青)は誤差-5〜+3の範囲に分布
- データ全体(100%)(水色)は誤差-20〜+9の範囲に分布
色が見えなくなっている部分は、赤に近い側の色の裏に隠れているものとして見てください。例えば6〜12手目では黄色が見えませんが、オレンジ色の裏に隠れているので95%以上のデータが-1〜+1の範囲に分布していることになります。なお、水色の部分は最小値〜最大値の範囲を表していることになりますが、選んだサンプルに偶々誤差の大きいものが入っているとぶれることになりますので、参考程度に見た方が良いと思われます。最後に、折れ線グラフは誤差の平均と標準偏差を表し、右側の軸で見ます。例えば、34手目〜40手目では、平均(実線)が0.04くらい、標準偏差(点線)が1.44くらいです。色を塗った時の見やすさの都合上、水平方向の点線(グリッド)は-0.1, 0, 0.1, 0.2, …ではなく、-0.05, 0.05, 0.15, 0.25, …の位置に引かれているので注意してください。
ちょっと複雑でしたが箱ヒゲ図よりも分布の様子が見えてきました。全データの99%を表している青のエリアに着目してみると、手が進んでいくごとに分布範囲が広がっています。黄色やオレンジ色に着目しても広がっています(黄色のマイナス側は最後はやや狭まったようですが)。同じ深さの読みで、同じselectivityの値であれば、中盤・終盤と進むほど誤差が大きくなるようです。
深さ・selectivityによる誤差の分布の変化
深さ15・selectivity73%で分布の様子を見てきましたが、selectivityを87%, 95%, …と上げていくと分布の様子はどう変わるのでしょうか?当然誤差は小さくなるはずです。一方、深さによる違いはどうでしょうか?直感的には読みが深くなるほど先で起こる変化も大きくなるように思いますが、それを考慮した上でEdaxが判断している可能性もありますので、何とも予想が難しいところです。
先ほどのグラフで横軸に何手目かを取っていましたが、深さとselectivityによる変化も見たくなってしまいました。軸が足りませんので、気合で先ほどの形式のグラフを深さとselectivityの分だけ並べてみることにしました。結果は以下の通りです。
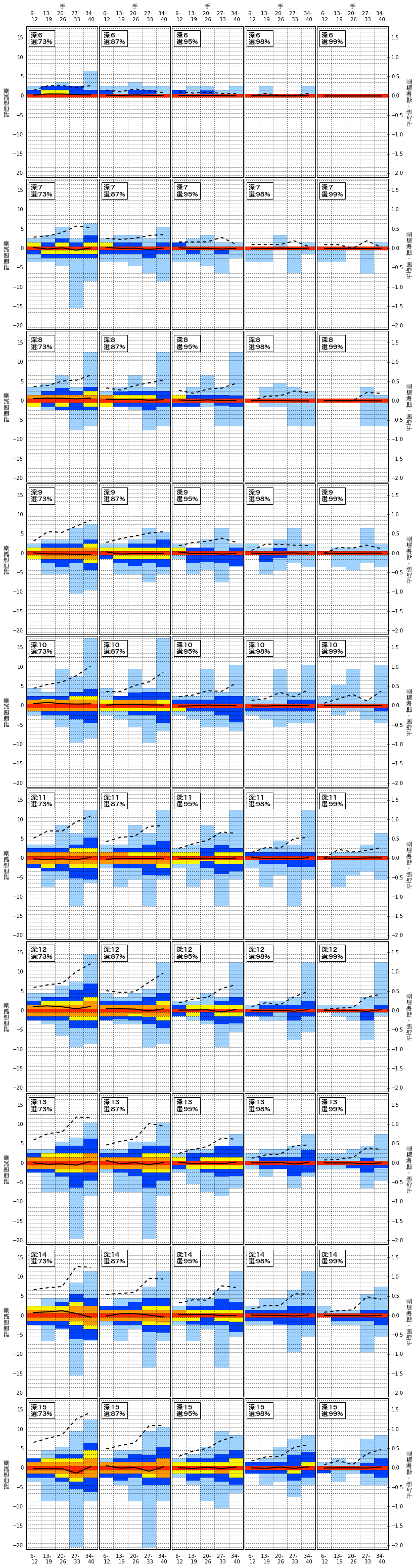 壮観ですね。深さ10パターン×selectivity5パターンの計50個のグラフが並んでいます。先ほどまで見ていた深さ15・selectivity73%のグラフは一番左下のものです。
壮観ですね。深さ10パターン×selectivity5パターンの計50個のグラフが並んでいます。先ほどまで見ていた深さ15・selectivity73%のグラフは一番左下のものです。
全体を眺めてみると、以下の傾向がわかります。
- 手が進むほど(1つ1つのグラフの中で右に行くほど)分布の範囲は広がる傾向にある
- 深さが深くなるほど(上のグラフから下のグラフに行くほど)分布の範囲は広がる傾向にある
- selectivityが73%→99%となるほど(左のグラフから右のグラフに行くほど)分布の範囲は狭まる傾向にある
分布の平均値は概ね0前後を保っているようですが、分布が広がって精度が悪くなっているようです。
深さに着目して再整理
本質的には先ほどのグラフと同じことですが、深さが深くなるとどれくらい精度が悪化しているかの様子をよりわかりやすく見るために、横軸に深さをとったグラフにして、代わりに何手目かについてはグラフをたくさん描くことでカバーしてみました。上の方が序盤のグラフ、下に行くほど中・終盤のグラフです。
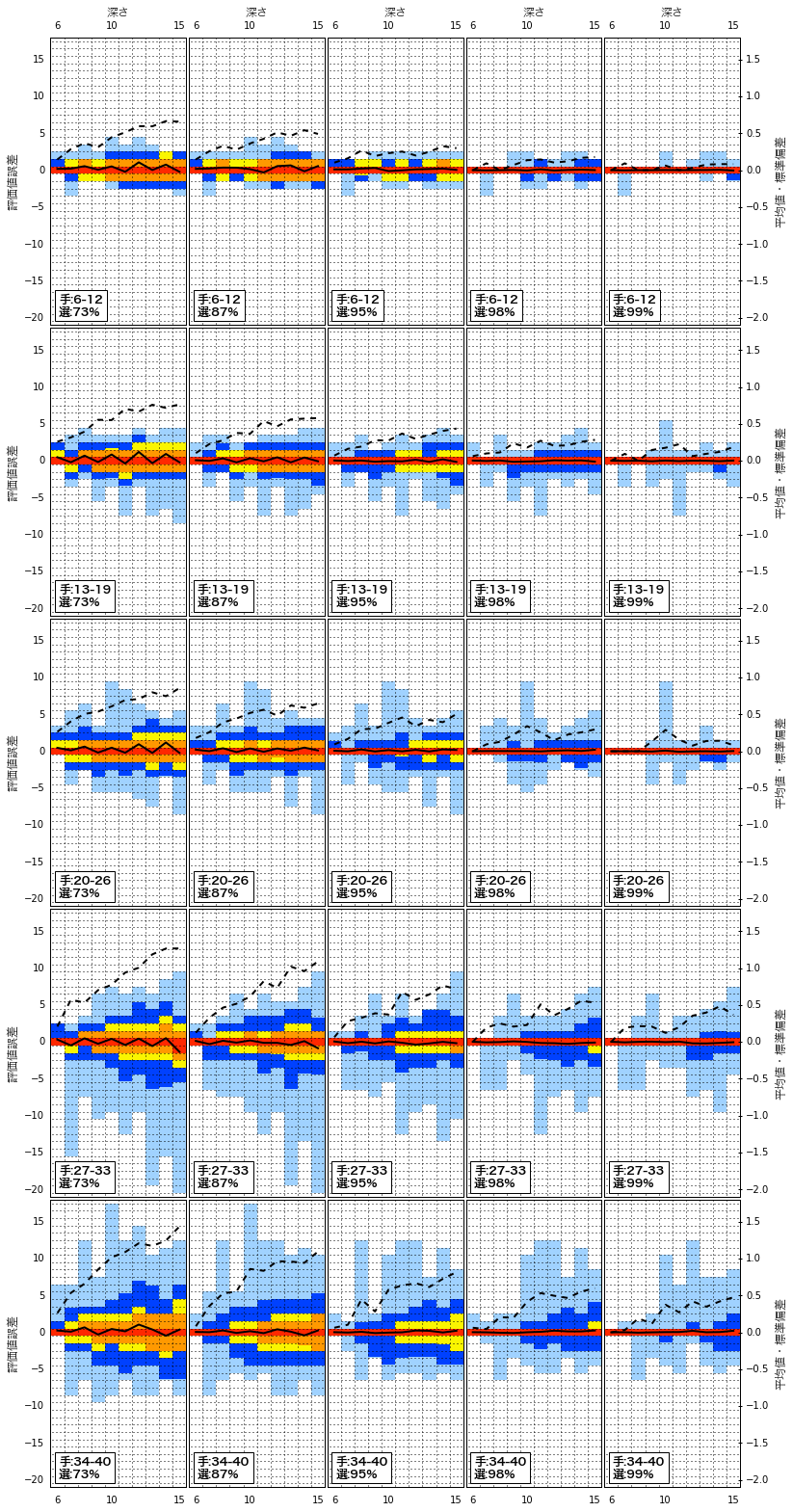
深さが深くなるにつれて分布が広がる様子がよりよくわかるようになりました。分布の広がりが頭打ちにならないか期待していたのですが、そうでもないようです。
さて、ここでレベルの意味を振り返ってみると、実用上使われることが多いと思われるレベル20前後で、Edaxで実際に使われている深さとselectivityの組み合わせは以下のようになっています。
- 30手目前後までは、深さはレベルの値(20前後)で、selectivity=73%
- 30手目前後以降は、深さは最終手まで(30前後以上)で、selectivity=73%〜
具体的に見てみたいので、ここではレベル=20を見てみることにします。レベル=20の場合は以下の通りです。
- 30手目まで、深さ=20・selectivity=73%
- 31〜33手目まで、深さ=30〜28(最終手まで)・selectivity=87%
- 34〜36手目まで、深さ=27〜25(最終手まで)・selectivity=98%
- 37手目以降、完全読み
まず30手目まではselectivity=73%なので、一番左側に並んでいるグラフになります。30手目までなので、一番上の段から4段目までが該当します。深さは20ですが、残念ながら深さ15までしかグラフがないので、20まで右に伸びていたらどうなるかを予想するしかありません。4段目の27〜33手目のグラフの深さ15のところでは、95%のデータが-3〜+2、99%のデータが-5〜+3の範囲に分布しているので、あと5深く読むことでもう少し(感覚的にはあと1〜2ずつくらい?)分布が広がると予想されます。
31〜33手目はselectivity=87%なので、左から2番目・下から2番目のグラフです。これの深さ=30〜28を予想することになります。73%の時よりは分布が狭まっているものの、深さ30くらいまでいくと分布はそれなりに広がっているのではないかと考えられます。見えている範囲から遠いので予想が難しいですが、感覚で黄色いエリアで±5前後、青いエリアで±8くらいと予想します(特に根拠はありません・・・)。
34〜36手目はselectivity=98%なので、右から2番目・一番下のグラフです。これの深さ=27〜25の予想になります。深さ15の時点では31〜33手目のグラフより大分狭い分布になっていて、この先の深さも27〜25までですから、31〜33手目の時よりは精度が良いものと予想されます。34手目以降については、深さ15の時点で計算時間がそこまでかかっていたわけではないので、34手目以降に絞ってさらに深く再計算させてグラフを作ってみました。
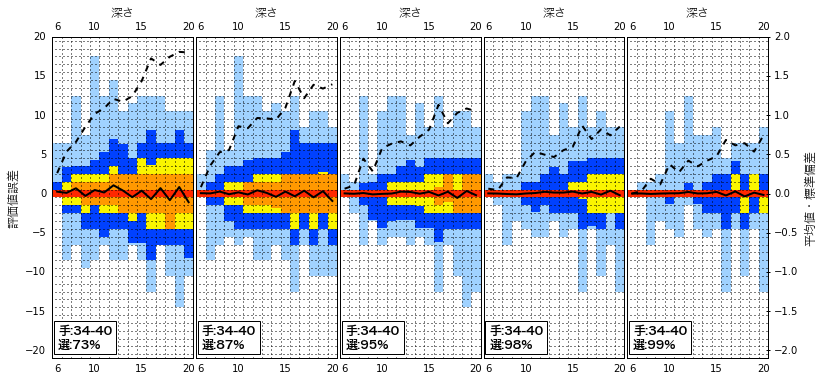 深さ20あたりで半日以上時間がかかるようになってしまったので、ここで断念しました。やはりじわじわと分布が広がってきています。深さ25まで届きませんでしたが、感覚的には黄色いエリアで±4くらい、青いエリアで±6くらいでしょうか。
深さ20あたりで半日以上時間がかかるようになってしまったので、ここで断念しました。やはりじわじわと分布が広がってきています。深さ25まで届きませんでしたが、感覚的には黄色いエリアで±4くらい、青いエリアで±6くらいでしょうか。
37手目以降は完全読みなので、当然selectivityによる誤差は発生しません。
レベル20について、selectivityによる誤差がどれくらいかをざっくりと見積もってみましたが、ご興味のある方はよく使われているレベルについて見積もってみてください(すでに文が長くなりすぎて、誰も読んでいないような気もしますが・・・)
補足
評価値の精度について
今回はselectivityによる評価値の精度の変化を見てみました。少し紛らわしい部分があるので整理しておきますが、評価値の精度は、
- 0手読みの評価値(評価関数)
- 読みの深さ
- selectivity
によって決まります。今回はselectivityによる影響が、序盤なのか中盤なのかや、読みの深さによって変わる様子がわかりました。特に深さが深くなるほどselectivityの影響が大きく(精度が悪く)なりました。これはもちろん、同じ読みの深さのselectivity=100%と比較したときの精度の変化であって、深読みするほど評価値の精度が悪くなると言っているわけではないことに注意する必要があります。もう少しわかりやすく言うと、
- 深さ=10、selectivity=73%
- 深さ=10、selectivity=100%
- 深さ=15、selectivity=73%
- 深さ=15、selectivity=100%
で計算した評価値について、2→1で悪くなる度合いと、4→3で悪くなる度合いを比べると、4→3の方がより悪くなるということを今回の結果は言っています。1と3を比べて1の方が精度が良いと言っているわけではありません。1と3ではより深く読んでいる3の方が当然精度が良いことが期待されますので、誤解のないようご注意ください。
局面の評価値と手の評価値
今回計算したのは、局面の評価値です。つまりその局面で最も良い手の評価値です。局面の評価値について、selectivityを変えて100%のものと比較して精度を調べました。注意する必要があるのは、例えばselectivity=73%で計算した時の最善手と、selectivity=100%で計算した時の最善手は必ずしも同じではないということです。つまり、特定の一手に着目した時の手の評価値の精度とは異なります。ただ、特定の一手に着目する場合は、その一手を打った次の局面で深さを一手分減らした評価値を考えれば良いので、今回の実験結果を深さ一手分減らすことで読み替えることができるはずです。
Edaxが間違いやすい局面
selectivityで誤差の大きくなる局面は、Edaxが間違いやすい局面だとも言えます。今回、深さ=14・selectivity=73%の探索結果の中で、レベル14で実際に使われる深さ・selectivityの組み合わせの局面から、誤差が最大・最小のものを調べてみました。まず最大のものですが、1992年の清水裕希子さんと広地正樹さん(両者とも段級位はわかりませんでした。ジュニア部門の結果のようです)の33手目の局面でした。
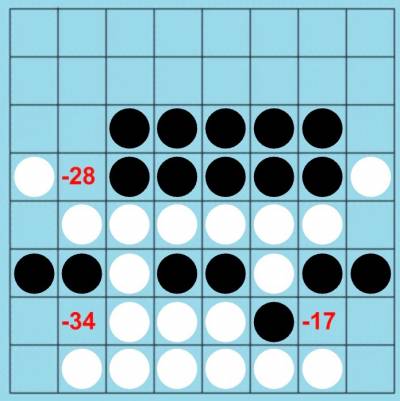 白の広地さんがa4と打った局面ですが、Edaxのレベル14(深さ=14,selectivity=73%)の推奨手はg7で-17となっています。しかし、selectivity=100%で読んでみると、この局面の最善手がg7であることは変わりませんでしたが、評価値は-25となりました。selectivityにより+8ずれてしまった(楽観的な読みになった)ことになります。
白の広地さんがa4と打った局面ですが、Edaxのレベル14(深さ=14,selectivity=73%)の推奨手はg7で-17となっています。しかし、selectivity=100%で読んでみると、この局面の最善手がg7であることは変わりませんでしたが、評価値は-25となりました。selectivityにより+8ずれてしまった(楽観的な読みになった)ことになります。
最小だったのは2016年の棋譜で、大清水崇典六段と村上健九段の対局の28手目の局面でした。
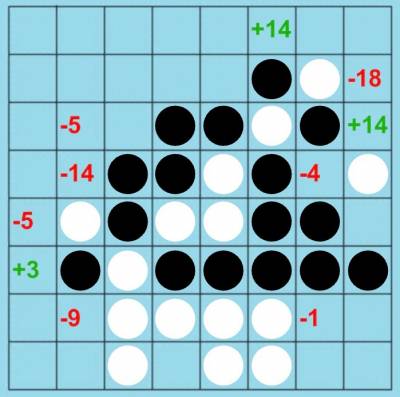 黒の大清水六段がg6と打った局面です。Edaxのレベル14は+14でf1を推しています。同じく+14でh3となっていました。selectivity=100%で読んでみると、この局面の最善手はh3で評価値は+29でした。selectivity=73%の時の誤差は-15となり、かなり悲観的な読みになっています。
黒の大清水六段がg6と打った局面です。Edaxのレベル14は+14でf1を推しています。同じく+14でh3となっていました。selectivity=100%で読んでみると、この局面の最善手はh3で評価値は+29でした。selectivity=73%の時の誤差は-15となり、かなり悲観的な読みになっています。
これらの局面は、Edaxが読みを進める途中の局面で、その時点の途中の評価と末端の局面で差が思いの外大きいものがあることになりますが、私の棋力ではどこがそうなっているのかはよくわかりませんでした。これをきちんと分析できれば、Edaxの弱点がわかるのかもしれません。
なお、大清水六段対村上九段の対局については、村上九段のブログに自戦解説がありましたので、興味のある方はぜひお読みください。
結論
長くなりました。あまりまとまりがないですが、無理やりまとめてみます。
- Edaxの%はselectivityと呼ばれるもので、見込みの少ない分岐の読みを打ち切る際の基準となる確率を表している
- 打ち切らなかった場合との誤差は、序盤よりは中終盤が、浅い読みよりは深い読みが大きくなりやすい
- その誤差は、実用的な範囲内では95%以上は±5くらいに収まりそう(予想)
コメント
こんにちは。 大変素晴らしい記事、ありがとうございます。 今まで見たedaxについての記事の中でもダントツに優れています。 かなり参考になりました。
もしよろしければ、今度bookの生成ロジックについてもご解説いただけると嬉しいです。
コメントどうもありがとうございます。
bookについてもいろいろわからないことがあるので、ちょうど調べているところでした。
仕組みがわかったら書いてみようと思います。
ありがとうございます。楽しみにしています!